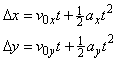Projectile Motion

You have probably watched a ball roll off a table and strike the floor. What determines where it will land? Could you predict where it will land? In this experiment, you will roll a ball down a ramp and determine the ball’s velocity with two Photogates. You will use this information and your knowledge of physics to predict where the ball will land when it hits the floor.

Figure 1

objectives

· Measure the velocity of a ball using two Photogates.

· Apply concepts from two-dimensional kinematics to predict the impact point of a ball in projectile motion.

· Take into account trial-to-trial variations in the velocity measurement when calculating the impact point.

Materials

TI Graphing Calculator	masking tape
LabPro or CBL2 interface	plumb bob
DataGate program	ramp
Vernier Photogate	ring stand
target	right-angle clamp
ball (1- to 5-cm diameter)	meter stick or metric measuring tape

Preliminary questions

1. If you were to drop a ball, releasing it from rest, what information would be needed to predict how much time it would take for the ball to hit the floor? What assumptions must you make?

2. If the ball in Question 1 is traveling at a known horizontal velocity when it starts to fall, explain how you would calculate how far it will travel horizontally before it hits the ground.

3. When an object passes through the Photogates, it blocks the passage of light from one side to the other. The interface can accurately measure the duration of time that the first gate is blocked until the second gate is blocked. If you wanted to know the velocity of the object, what additional information would you need?

Procedure

1. Set up a low ramp made of angle molding on a table so that a ball can roll down the ramp, across a short section of table, and off the table edge as shown in Figure 1.

2. Position the Photogates so the ball rolls completely through both gates while rolling on the horizontal table surface (but not on the ramp). Center the detection line of the gate on the middle of the ball. Connect the Photogate to the Ch 1 port of the CBL  or the DIG/SONIC 1 port of the LabPro interface. To prevent accidental movement of the Photogate, you can use tape to secure the ringstand in place. Use the link cable to connect the TI Graphing Calculator to the interface. Firmly press in the cable ends.

3. Mark a starting position on the ramp so that you can repeatedly roll the ball from the same place. Roll the ball down the ramp through the Photogates. Stop the ball before it leaves the table. Note: Do not let the ball hit the floor during these trials, or during the following velocity measurements. Make sure that the ball does not strike the side of the Photogate. Move the Photogate if necessary.

4. Measure the distance between the center’s of the Photogates as carefully as possible. The accuracy of the rest of the experiment depends on this single measurement. You must know the distance, Dx, in order to calculate the velocity of the ball as it passes through the gates. You will divide this distance by the time interval Dt measured by the interface to get the ball’s velocity (v = Ds/Dt). To successfully predict the impact point, you must have an accurate diameter measurement. Record the diameter in your Data Table.

5. Turn on the calculator and start the DATAGATE program.

6. Observe the reading on the calculator screen. Block the Photogate with your hand; note that the Photogate is shown as blocked (--X--) on the calculator screen. Remove your hand and the display should change to unblocked (--0--).

7. The calculator will measure the length of time the photogate is blocked. You can see how this works by the gate briefly with your hand. Prepare the calculator to do this.

a. Select START from the main screen.

b. Block the gate with your hand for about one second, and then remove your hand from the gate.

8. Note that the calculator now shows a time interval in seconds. This is the length of time that the gate was blocked. Prepare the calculator to measure another interval.

a. Press to end data collection.

b. Select START to perform another time measurement.

9. Roll the ball from the mark on the ramp, through the Photogate, and catch the ball immediately after it leaves the table. Record each time interval in the Data Table. Repeat nine times. After the last trial, press to end data collection.

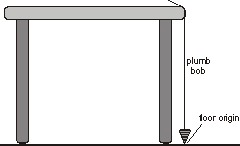
Figure 2

10. Inspect your time data. Did you get the same value every time? From your time intervals and the ball diameter, determine the velocity of the ball for each trial. Determine the average, maximum, and minimum velocities, and enter them in your Data Table. What one value would be most representative of all ten measurements?

11. Carefully measure the distance from the tabletop to the floor and record it as the table height h in the Data Table. Use a plumb bob to locate the point on the floor just beneath the point where the ball will leave the table. Mark this point with tape; it will serve as your floor origin.

12. Use your average velocity value to calculate the distance from the floor origin to the impact point where the ball will hit the floor. You will need to algebraically combine relationships for motion with constant acceleration

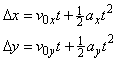
First, simplify the equations above. What is the value of the initial velocity in the vertical direction (v_0y)? What is the acceleration in the horizontal direction (a_x)? What is the acceleration in the vertical direction (a_y)? Remember that the time the ball takes to fall is the same as the time the ball flies horizontally. Use this information and the simplified equations to calculate how far the ball should travel horizontally during the fall. Record the value in your Data Table as the predicted impact point.

Mark your predicted impact point on the floor with tape and position a target at the predicted impact point. Be sure the impact point is along the line of the track.

13. To account for the variations you saw in the Photogate velocity measurements, repeat the calculation in the preceding step for the minimum and maximum velocity. These two additional points show the limits of impact range that you might expect, considering the variation in your velocity measurement. Mark these points on the floor as well, and record the values in your Data Table.

14. After your instructor gives you permission, release the ball from the marked starting point, and let the ball roll off the table and onto the floor. Mark the point of impact with tape. Measure the distance from the floor origin to the actual impact and enter the distance in the Data Table.

Data Table

Trial	Time	Velocity
	(s)	(m/s)	Ball diameter	m
1			Maximum velocity	m/s
2			Minimum velocity	m/s
3			Average velocity	m/s
4			Table height	m
5			Predicted impact point	m
6			Minimum impact point distance	m
7			Maximum impact point distance	m
8			Actual impact point distance	m
9
10

Analysis

1. Should you expect any numerical prediction based on experimental measurements to be exact? Would a range for the prediction be more appropriate? Explain.

2. Was your actual impact point between your minimum and maximum impact predictions? If so, your prediction was successful.

3. You accounted for variations in the velocity measurement in your range prediction. Are there other measurements you used which affect the range prediction? What are they?

4. Did you account for air resistance in your prediction? If so, how? If not, how would air resistance change the distance the ball flies?

Extensions

1. Derive one equation for the horizontal and vertical coordinates of the ball’s motion in this experiment.

2. Derive a general formula for projectile motion with the object launched at an angle.

3. Increase the challenge by placing a ring on a ring stand part way to the eventual target. The ball must pass through the ring successfully and then hit the target. You are required to position the ring as well as the target on the floor.

4. (LabPro only) Use a second Photogate to measure the speed of the ball. Instead of using the ball diameter, measure the distance between the Photogates. Use the time between blocks of the two gates to calculate the ball’s speed.